Lec 3 - Basis & Higher Dimensions
Monday, January 09, 2012
9:24 AM
![]()
![]()
![]() Q: How do
we find the smallest spanning set?
Q: How do
we find the smallest spanning set?
![]()
![]()
Definition
A set of vectors is linearly dependent if one vector in the set is a linear combination of the remaining vectors.
Otherwise, the set of vectors is linearly independent.
![]() Is there
a nice mathematical expression to define linear dependence?
Is there
a nice mathematical expression to define linear dependence?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Better Definition
![]()
![]()
![]()
![]()
![]()
Proof:
![]()
![]()
![]()
Q.E.D.
Eg.
![]()
Consider the equation
![]()
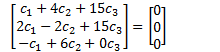
We have 3 equations and 3 unknowns:
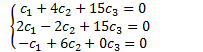
![]()
Sub into equation 1:
![]()
![]()
Our set is linearly dependent.
![]() Note: In
order for a spanning set to be as small as possible, it must be linearly
independent.
Note: In
order for a spanning set to be as small as possible, it must be linearly
independent.
Definition
![]()
![]()
Ex.
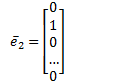
![]()
Eg.
![]()
![]() Surfaces
in Higher Dimensions
Surfaces
in Higher Dimensions
Definition
![]()
![]()
![]()
![]()
![]()
![]() Subspaces
Subspaces
For a set of vectors to be closed under linear combinations, we must be able to apply the operations of vector addition and scalar multiplication.
Definition
![]()
![]()
![]()
Definition
![]()